L-BFGS Method

What is L-BFGS

Member of the quasi-newton methods family
It is a whole batch optimization method
The memory limited version of BFGS
It is a method of approximating the hessian matrix
The BFGS stores an nxn Hessian matrix
L-BFGS stores only a few vectors
Well suited for optimizations with many variables

Figure 1: Broyden, Fletcher, Goldfarb and Shanno from left to right.

How to use it?

Here we are going to use an implementation of L-BFGS in PyTorch to minimize the Rosenbrock function.

What is Rosenbrock function?

Rosenbrock function is a non-convex function which its' global minima is inside a long narrow valley which is trivial to find, but converging to the global minima inside that valley is a difficault task. \[f(x,y) = b(y-x^2)^2 + (a-x)^2\] where \(a\) and \(b\) are constants. The global minima is at \((a,a^2)\). It is mostly used as a benchmark for optimization algorithms.

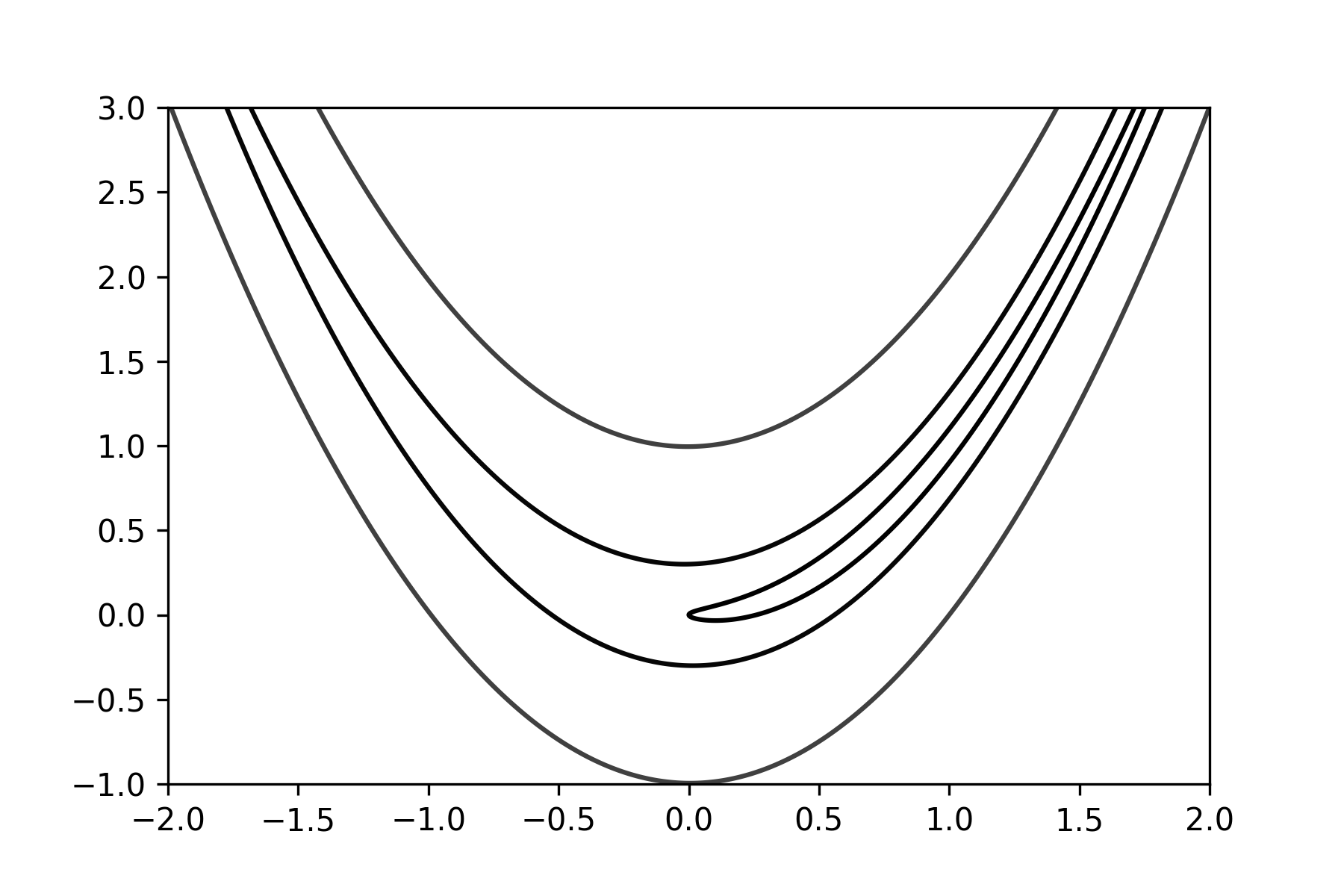
a contour plot of the Rosenbrock function

Figure 2: Rosenbrock function

What is a closure function?

Some Optimizers in PyTorch such as Conjugate Gradient and LBFGS require a closure function to be passed to them. A closure function is a function that at first clears the gradients, computes the loss, and reevaluates the function.

    
        def closure():
            optimizer.zero_grad()
            loss.backward()
            return loss.item()

Define a custom function in PyTorch

In order to be able to use the optimizers implemented in pytorch to minimize a function, we have to redefine that function as a class like we do for different Neural Networks in PyTorch.

        
class Rosenbrock(nn.Module):
    def __init__(self, a, b):
        super(Rosenbrock, self).__init__()
        # Initializing the Rosenbrock function
        self.a = a
        self.b = b
        # Optimization parameters are randomly initialized and
        # defined to be a nn.Parameter object.
        self.x = torch.nn.Parameter(torch.Tensor([-1.0]))
        self.y = torch.nn.Parameter(torch.Tensor([2.0]))

    def forward(self,):
        # Here is the function that is being optimized
        return (self.x - self.a) ** 2 + self.b * (self.y - self.x ** 2) ** 2

Note the difference between how we define constants and optimization variables. Then the optimizer can be initialized like this:

        
optimizer = torch.optim.LBFGS(model.parameters(), lr=0.1, max_iter=5000)

Here is the gif of the convergence steps:

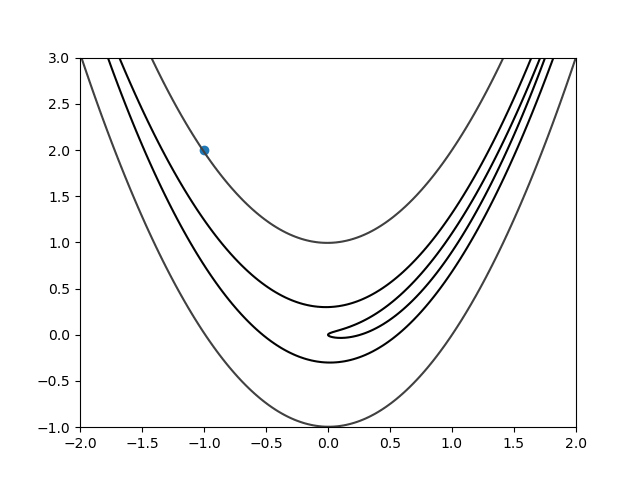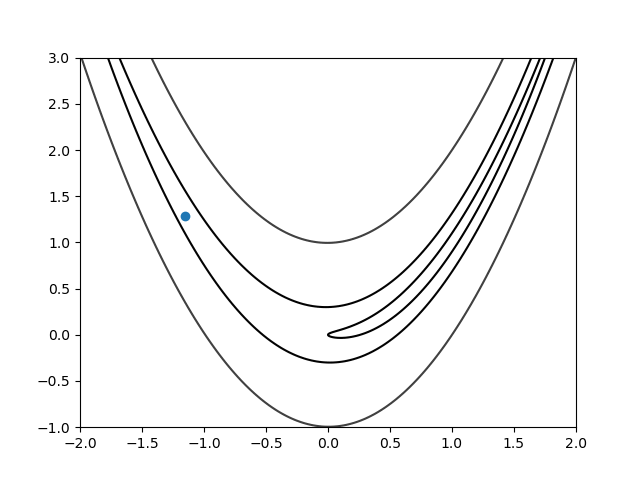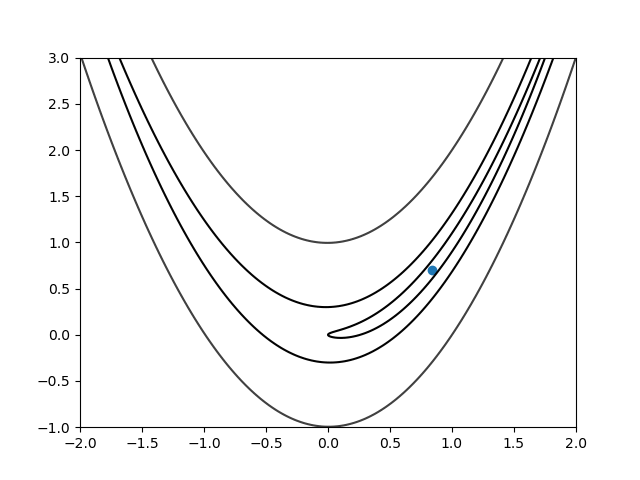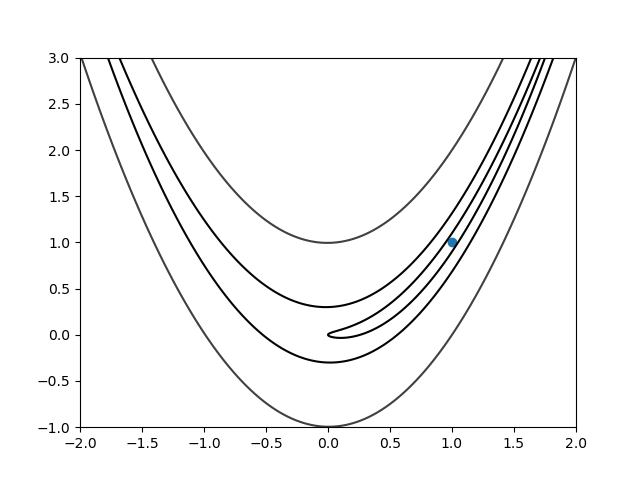
Figure 3: Convergence Steps (wait for it)

you can find all the related codes inside this github repository.