Figure 1: set of base point.
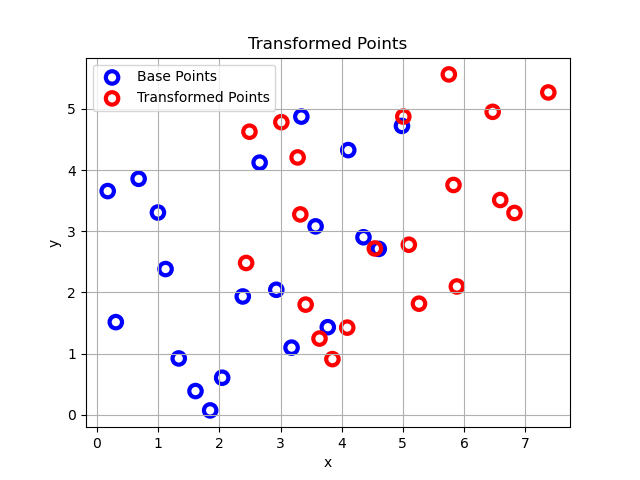
Figure 2: both sets of points.

Figure 1: set of base point.

Figure 2: both sets of points.
Assume that we have two point sets {p_i} and {p'_i} \[p'_i = R p_i + T\] where R is a 3x3 rotation matrix and T is a 3x1 translation vector. we can formulate a minimization problem to find \(R\) and \(T\) as follows: \[\min_{R,T} \sum_{i=1}^{n} \|p'_i - R p_i - T\|^2\] If the solution to the least square problem is \(\hat{R}\) and \(\hat{T}\), then the centroid of point set {p"_i} and {p_i} are the same. \[p"_i = \hat{R} p_i + \hat{T}\] If we name the centroids of the two point sets as \(p_c\) and \(p'_c\), then we can translate the centroid of all the pointsets to the origin and then the points would be like this: \[q_i = p_i - p_c\] \[q'_i = p'_i - p'_c\] now the original minimization problem is formulated as a least square problem: \[\min_{R,T} \sum_{i=1}^{n} \|q'_i - R q_i\|^2\] Then all we have to do is to find \(R\) by solving the above least square problem using SVD decomposition and then we can simply find \(T\) by putting the \(R\) into this equation: \[\hat{T} = p' - \hat{R}p\] In order to do that we first define the matrix H like this: \[H = q_i\dot q'_i\] Then we can find the SVD decomposition of H like this: \[H = U S V^T\] Then we get \(X\) to be: \[X = VU^T\] Then we have to calculate the determinant of X; if it was +1 then \(X\) is the rotation matrix we have been looking for! if it was -1 then the algorithm has failed which is not so likely to happen.
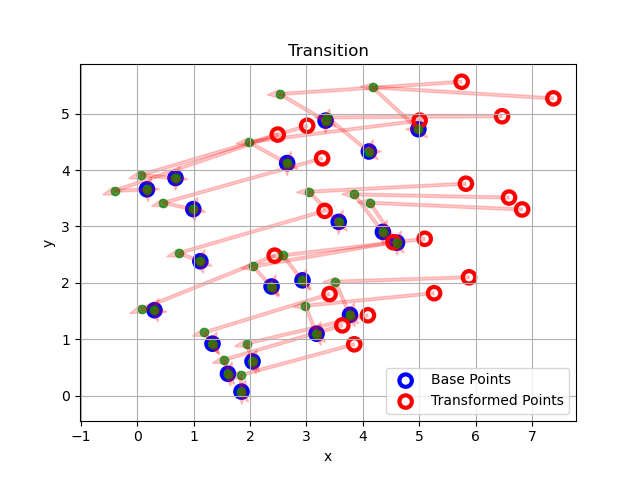
Figure 3: trajectory of transformation.
you can find an implementation of it in my github repository along with all the figures.